Difference between revisions of "ALGORITHM2"
(Created page with "caption [Home] - [Algorithms] ---- '''HASARD''' is a probabilistic flood mapping algorithm developed by [https:/...") |
|||
| (30 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
---- | ---- | ||
| − | + | [https://www.dlr.de/ DLR]'s flood detection algorithm (provisionally, '''Algorithm2''') is a [https://it.wikipedia.org/wiki/Fuzzy_Logic fuzzy logic]-based water class membership assignment, described in Martinis et al. (2015)<sup>[1]</sup> and Twele et al. (2016)<sup>[2]</sup>. <br> | |
| − | + | It aims to exclude water-lookalikes and to reduce underestimations from initial classification by constructing a fuzzy set that consists of: | |
| − | + | *(a) the backscatter level | |
| − | + | *(b) the elevation of an image element in comparison to the mean elevation of the initially derived water areas | |
| + | *(c) topographic slope information | ||
| + | *(d) the size of an individual flood object; degree of an element’s membership to the class water is determined by standard S and Z membership functions. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The average of the individual membership degrees is computed for each pixel in order to combine all fuzzy elements into a single composite fuzzy set (see figure below). | |
| − | The | + | |
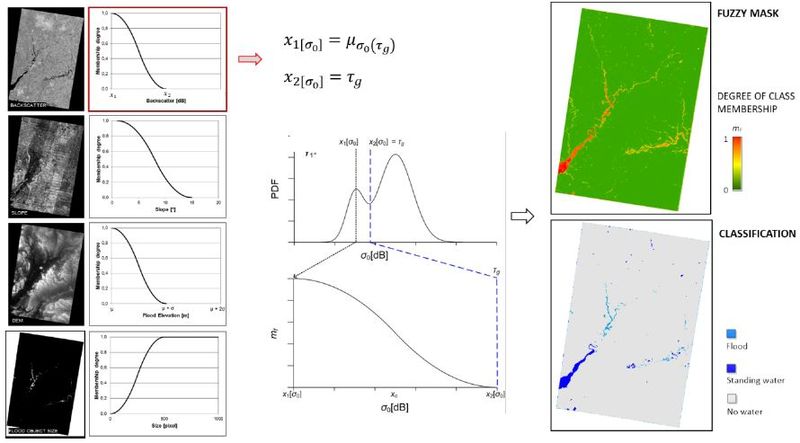
| − | + | [[File:alg2.jpg|centre|800px|border]] | |
| − | + | ''The automatic tile-based thresholding procedure is applied to a given SAR image to select for representative tiles therein. A sub-histogram is generated for a selected tile, based on the backscatter values, one of the parameters of the fuzzy set (left); the corresponding fuzzy standard Z function for backscatter is shown (middle), along with the resulting fuzzy mask and classification maps (right; adapted from Martinis et al. (2015)<sup>[1]</sup>).'' | |
| + | |||
| + | The membership degree strongly depends on the position of the crossover point xc (i.e. the half of the width of the fuzzy curve), which is defined by the fuzzy thresholds ''x1'' and ''x2''.The fuzzy threshold values for each element are either determined according to statistical computations or are set empirically. The membership degree of the subsequently, the flood mask is derived through a threshold defuzzification step, which transforms each image element with a membership degree > ''0.6'' into a discrete thematic class. Furthermore, the region-growing tolerance criterion is defined by a relaxed fuzzy threshold of > ''0.45'' based on the composite fuzzy set. | ||
| + | Uncertainty information is contained in the fuzzy mask generated over classified water pixels, which takes on values ranging from ''0'' and ''1''. | ||
| + | |||
| + | |||
| + | ====<u>''Workflow of the algorithm''</u>==== | ||
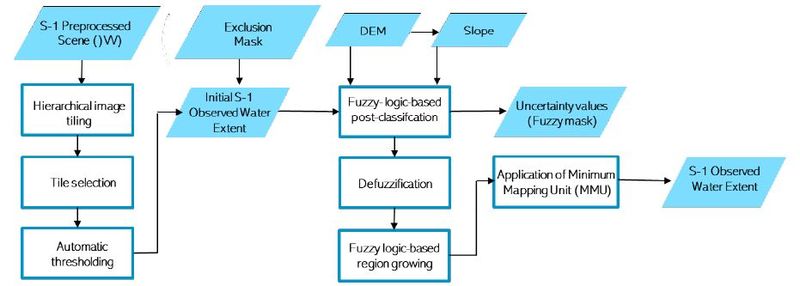
| + | [[File:alg2_wf.jpg|centre|800px|border]] | ||
| + | |||
| + | |||
| + | ====<u>''In a nutshell''</u>==== | ||
| + | The key strength of '''Algorithm 2''' is the automatic identification of flooded areas in the SAR data using '''hierarchical tile-based thresholding''' and the optimization of the classification by combining various information sources using '''fuzzy-logic theory''' and '''region growing'''. | ||
| Line 24: | Line 32: | ||
| − | |||
====<u>''References''</u>==== | ====<u>''References''</u>==== | ||
| − | <sup>[1]</sup> | + | <sup>[1]</sup> [https://www.sciencedirect.com/science/article/pii/S0924271614001981 <u>Martinis, S., Twele, A., Kersten, J., (2015). A fully automated TerraSAR-X based flood service. ISPRS Journal of Photogrammetry and Remote Sensing, 104, 203-212.</u>] <br> |
| − | |||
| − | <sup>[2]</sup> | + | <sup>[2]</sup> [https://www.tandfonline.com/doi/abs/10.1080/01431161.2016.1192304 <u>Twele, A., Cao, W., Plank, S., Martinis, S., 2016. Sentinel-1 based flood mapping: a fully automated processing chain. International Journal of Remote Sensing, 37 (13), 2990-3004.</u>] |
| − | |||
---- | ---- | ||
[[GFMS | [Home]]] - [[ALGORITHMS | [Algorithms]]] | [[GFMS | [Home]]] - [[ALGORITHMS | [Algorithms]]] | ||
Latest revision as of 11:11, 10 March 2021
DLR's flood detection algorithm (provisionally, Algorithm2) is a fuzzy logic-based water class membership assignment, described in Martinis et al. (2015)[1] and Twele et al. (2016)[2].
It aims to exclude water-lookalikes and to reduce underestimations from initial classification by constructing a fuzzy set that consists of:
- (a) the backscatter level
- (b) the elevation of an image element in comparison to the mean elevation of the initially derived water areas
- (c) topographic slope information
- (d) the size of an individual flood object; degree of an element’s membership to the class water is determined by standard S and Z membership functions.
The average of the individual membership degrees is computed for each pixel in order to combine all fuzzy elements into a single composite fuzzy set (see figure below).
The automatic tile-based thresholding procedure is applied to a given SAR image to select for representative tiles therein. A sub-histogram is generated for a selected tile, based on the backscatter values, one of the parameters of the fuzzy set (left); the corresponding fuzzy standard Z function for backscatter is shown (middle), along with the resulting fuzzy mask and classification maps (right; adapted from Martinis et al. (2015)[1]).
The membership degree strongly depends on the position of the crossover point xc (i.e. the half of the width of the fuzzy curve), which is defined by the fuzzy thresholds x1 and x2.The fuzzy threshold values for each element are either determined according to statistical computations or are set empirically. The membership degree of the subsequently, the flood mask is derived through a threshold defuzzification step, which transforms each image element with a membership degree > 0.6 into a discrete thematic class. Furthermore, the region-growing tolerance criterion is defined by a relaxed fuzzy threshold of > 0.45 based on the composite fuzzy set. Uncertainty information is contained in the fuzzy mask generated over classified water pixels, which takes on values ranging from 0 and 1.
Workflow of the algorithm
In a nutshell
The key strength of Algorithm 2 is the automatic identification of flooded areas in the SAR data using hierarchical tile-based thresholding and the optimization of the classification by combining various information sources using fuzzy-logic theory and region growing.
For further details the Reader is referred to the dedicated section of the Product Description Document: https://www.gfm_pdd.org/Algorithm2
References